Unfinished Business
I have been on a math kick recently, having rediscovered math in last year’s experiment in retaking the SATs after a 40 year hiatus. (See prior posts filed under “SAT Experience.”) A previous essay described my quest to finally understand why you can’t divide by zero (Grokking It), but now I realize that I have one piece of unfinished business left from my junior high school education. How is it that multiplying two negative numbers results in a positive number? It makes no intuitive sense to me, because as I was taught early and often – two wrongs do not make a right.
My journey through the history of zero taught me that math is best understood if you can restrain yourself from trying to explain all math through real world problems. Basically, numbers are simply tools, and have no meaning aside from what we assign to them. The number “1” on its own doesn’t mean much, it is only when we say “one banana” that it acquires some sort of context. Aside from mathematicians, engineers and physicists, every day math for the everyday person is all about counting objects in our every day world, so that math as a concept is unfamiliar. So perhaps my multiplication problem should be reframed as a problem that does not have a simple real word explanation, and, just like dividing by zero, I should just accept it and move on.
And this is what I did, and it has served my very well. However, in the back of my mind, I have wondered how such a basic concept of life could be based on a rule without a rationale explanation. Certainly, the vast majority of my day passes in a “need to know” basis, starting from the light switch in the morning, to the telephone, and of course the internet. I have never understood electricity and can only visualize a swarm of little e–’s coursing through wires. And the internet is even more mysterious, grabbing information from an all-knowing invisible force and displaying it just for me on my screen. I choose not to understand these everyday conveniences and leave them to the engineers and physicists, but somehow multiplying two negative numbers seems to be so basic that it should be within my grasp.
Another theme that ran through my education was that if I didn’t understand something then it was probably my fault – perhaps I was sick on the day of the big explanation and AHA moment, or perhaps I was doodling, but my assumption was that everyone else understood the two negative numbers conundrum, and that I was the only one slavishly following a rule that I did not understand. And then of course there is only a window of time when you can raise your hand and say, “I’m sorry, I just don’t understand – it just doesn’t make any sense to me why -2 X -2 is 4.” Maybe you could ask this question in 8th grade, maybe 10th grade, but I can’t imagine raising my hand and asking it in college. At that point, by default I just had to live with the rule.
One of my bosses once gave me the advice, “it is better to be stupid than look stupid.” In other words keep your stupidity to yourself. This tip was given in regard to public presentations at the American Medical Association, where I was frequently put in the position of having to answer questions that I knew nothing about. Just better to deflect the question rather than flailing around and making an idiot out of yourself. So the real issue boils down to whether you are smart enough to know when you are stupid and should keep your mouth shut. I have fallen into that trap several times when my ignorance is so complete that I don’t even realize that I’m ignorant.
I play handbells at the local Presbyterian church, not because I am a Presbyterian, but because that is where the handbells are. I have always known that a yawning hole in my education is any knowledge of any religion. Sure I know about Christmas and Easter – although I don’t know why Easter is not on the same day every year, and what Lent is supposed to represent. Our choir performs before Christmas every year, and we always seem to perform “We Three Kings of Orient Are,” which is in some dreary and dissonant key. I asked, “Why can’t we play something peppier?” The choir looked at me with disbelieving eyes and said, “Because it is Advent.” Hmm – I wisely decided not to pursue this further, but then made the same mistake before Easter, when we similarly always play something downbeat. This time I got the same look, with the answer, “Because this is the Lenten season.” Now I wisely shut up and just play what is put in front of me. One time I went out to lunch with a Jewish colleague and offered to split a sandwich with him. He looked at me and said, “First of all, don’t you know that it is Passover, and second of all that during Passover I only eat unleavened bread.” I wanted to point out that I was totally unbiased and that my ignorance extended across all religions, but I was smart enough to know that professing complete ignorance should only be invoked if you are facing jail time.
So where do you go when the window is closed on stupid questions? You need a trusted nonjudgmental friend who answers even the most naïve questions with good karma. This was especially important in my medical career when I was in the position of interviewing physicians who were expert in their field. I needed a whole hierarchy of people I could call on to move me along the learning curve, so that I could hold my own when I finally interviewed the imperious Dr. Big. Often I found that the initial boost onto the learning curve was all I needed – I could make my way from there, but it could be challenging to find that first infinitely patient person.
But now I have a new BFF, it is called the internet, who seems to know everything and considers nothing too stupid. I type in “multiplying two negative numbers” and I discover that I am not alone, there are millions of people just like me who secretly feel either curious or inadequate and have turned to the internet for nonjudgmental comfort. Some entries explained the problem by using a different spin on the “two wrongs don’t make a right” adage, by stating that two negatives result in a positive statement, such as “I didn’t say that I don’t like you.” However, I reject that explanation, since, to me, this statement is more dissembling than a positive statement.
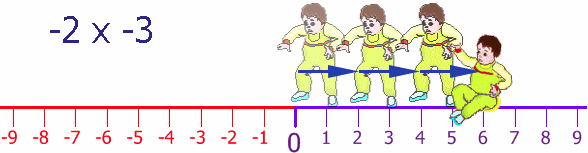
There were other attempts at real world explanation. The most creative was the baby walking backwards on the number line. Here is how you visualize it. The baby faces toward the west if there is a negative number. For example, if the problem is 2 X -3, he faces west (the negative number) and takes two paces three times and he ends up at the -6 position. Now, for -2 X -3, he again faces west, but this times he walks backwards 2 steps three times and ends up at the positive 6 spot.
Well maybe that makes some sense but I still think that it arbitrarily assigns which way the baby is facing and walking. A more real life explanation involves loans. Let’s say your employer automatically deducts your $1,000 mortgage payments from your monthly paycheck, i.e. $12,000 is removed from your paycheck every year (i.e. -1,000 x 12 = -12,000). Now let’s say that your company decides to give you a bonus by removing the deduction every month for a year – i.e. they deduct the deduction (get it, two negatives) and if you do that every month you end up with $12,000 additional dollars at the end of the year. Again this seems contrived to me. Ultimately, similar to zero, the best approach is just to stop using numbers and rely on symbols – that way you don’t have to remember which way the baby is walking or who owes who. So here is a purely mathematical approach to the issue:
——————————————-
Start out with the equation
x = ab + (-a)(b) + (-a)(-b)
And watch what happens when you solve it two different ways, first factoring out a, and then b.
Factoring out a we get:
x = ab + -a (b-b)
and since b-b = 0 our final answer is;
x = ab
Now let’s solve the same equation in a different way by factoring out b.
x = b (a-a) + (-a)(-b)
And since a-a = 0, our final answer is:
x = (-a)(-b)
Therefore, solving the same question two different ways we see that x = ab = (-a)(-b)——————————————–
Tah Dah! Finally, I have answered the question that I have been afraid to ask for 45 or so years. But watch out, I see that next chapter in my math book introduces the concept of i, defined as the square root of -1 ( i.e. √-1), which of course I have just convinced myself can’t possibly exist. An engineer named Rafael Bombelli came up with this in 1572, and this seems to be a nice place for me to stop refreshing my math skills. From this point forward, math wise, I am happy to be on a “need to know” basis.
The missing words in the following poem are two sets of anagrams (i.e. share the same letters like spot, stop and post) and the number of dashes and asterisks indicate the number of letters. One of the missing words in each set of anagrams will rhyme with either the preceding or following line. Your job is to solve the anagrams based on the above rules and the context of the poem. Scroll down for answers.
It has been an interesting form of recreation
As I have ****** through my long lost math education.
I wasn’t sure where my journey was ******
But I hoped to revisit some rules I had always doubted.
Geometry was well taught and I appreciated and all of its logical beauties,
But my teacher totally punted on his multiplication – – – – – – .
Specifically, why did multiplying two negatives result in a plus?
But it – – – – – – him to tell me only that it was a rule I could trust.
With blind obedience I learned the rule and have – – – – – – for the past 45 years
But I always wanted a proof to make multiplication perfectly clear.
So I took a ****** to the internet that showed me an equation manipulating a’s and b’s
And now I multiply two negatives with the utmost confidence and ease.
*
*
*
*
*
*
*
Answers: toured, routed, duties, suited, used it, detour